Monte Carlo tree search

In computer science, Monte Carlo tree search (MCTS) is a heuristic search algorithm for some kinds of decision processes, most notably those employed in game play. A leading example is recent computer Go programs, but it also has been used in other board games, as well as real-time video games and non-deterministic games such as poker (see history section).

Principle of operation

The focus of Monte Carlo tree search is on the analysis of the most promising moves, expanding the search tree based on random sampling of the search space. The application of Monte Carlo tree search in games is based on many playouts. In each playout, the game is played-out to the very end by selecting moves at random. The final game result of each playout is then used to weight the nodes in the game tree so that better nodes are more likely to be chosen in future playouts.

The most basic way to use playouts is to apply the same number of playouts after each legal move of the current player, then choosing the move which led to the most victories.

Selection: start from root $R$ and select successive child nodes down to a leaf node $L$ . The section below says more about a way of choosing child nodes that lets the game tree expand towards most promising moves, which is the essence of Monte Carlo tree search.
Expansion: unless $L$ ends the game with a win/loss for either player, either create one or more child nodes or choose from them node $C$ .
Simulation: play a random playout from node $C$ .
Backpropagation: use the result of the playout to update information in the nodes on the path from $C$ to $R$ .

Sample steps from one round are shown in the figure below. Each tree node stores the number of won/played playouts.

Steps of Monte Carlo tree search

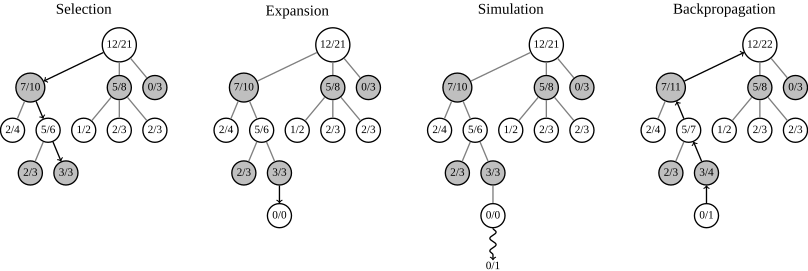
Note that the updating of the number of wins in each node during backpropagation should arise from the player who made the move that resulted in that node (this is not accurately reflected in the sample image above). This ensures that during selection, each player's choices expand towards the most promising moves for that player, which mirrors the goal of each player to maximize the value of their move.

Rounds of search are repeated as long as the time allotted to a move remains. Then the move with the most simulations made is selected rather than the move with the highest average win rate.

Pure Monte Carlo game search

This basic procedure can be applied to any game whose positions necessarily have a finite number of moves and finite length. For each position, all feasible moves are determined: k random games are played out to the very end, and the scores are recorded. The move leading to the best score is chosen. Ties are broken by fair coin flips. Pure Monte Carlo Game Search results in strong play in several games with random elements, as in EinStein würfelt nicht!. It converges to optimal play (as k tends to infinity) in board filling games with random turn order, for instance in Hex with random turn order.

Exploration and exploitation

The main difficulty in selecting child nodes is maintaining some balance between the exploitation of deep variants after moves with high average win rate and the exploration of moves with few simulations. The first formula for balancing exploitation and exploration in games, called UCT (Upper Confidence Bound 1 applied to trees), was introduced by Levente Kocsis and Csaba Szepesvári. Kocsis and Szepesvári recommend to choose in each node of the game tree the move, for which the expression 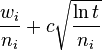$\frac{w_i}{n_i} + c\sqrt{\frac{\ln t}{n_i}}$ has the highest value. In this formula:

$w i$ stands for the number of wins after the $i$ -th move;
$n i$ stands for the number of simulations after the $i$ -th move;
$c$ is the exploration parameter—theoretically equal to $\sqrt2$ ; in practice usually chosen empirically;
$t$ stands for the total number of simulations for the node considered. It is equal to the sum of all the $n i$ .

The first component of the formula above corresponds to exploitation; it is high for moves with high average win ratio. The second component corresponds to exploration; it is high for moves with few simulations.

Most contemporary implementations of Monte Carlo tree search are based on some variant of UCT.

Advantages and disadvantages

Although it has been proved that the evaluation of moves in Monte Carlo tree search converges to minimax, the basic version of Monte Carlo tree search converges very slowly. However Monte Carlo tree search does offer significant advantages over alpha–beta pruning and similar algorithms that minimize the search space.

In particular, Monte Carlo tree search does not need an explicit evaluation function. Simply implementing the game's mechanics is sufficient to explore the search space (i.e. the generating of allowed moves in a given position and the game-end conditions). As such, Monte Carlo tree search can be employed in games without a developed theory or in general game playing.

The game tree in Monte Carlo tree search grows asymmetrically as the method concentrates on the more promising subtrees. Thus it achieves better results than classical algorithms in games with a high branching factor.

Moreover, Monte Carlo tree search can be interrupted at any time yielding the most promising move already found.

Improvements

Various modifications of the basic Monte Carlo tree search method have been proposed to shorten the search time. Some employ domain-specific expert knowledge, others do not.

Monte Carlo tree search can use either light or heavy playouts. Light playouts consist of random moves while heavy playouts apply various heuristics to influence the choice of moves.

Patterns of hane (surrounding opponent stones) used in playouts by the MoGo program. It is advantageous for both black and white to put a stone on the middle square, except the rightmost pattern where it favors black only.

Domain-specific knowledge may be employed when building the game tree to help the exploitation of some variants. One such method assigns nonzero priors to the number of won and played simulations when creating each child node, leading to artificially raised or lowered average win rates that cause the node to be chosen more or less frequently, respectively, in the selection step.

The basic Monte Carlo tree search collects enough information to find the most promising moves only after many rounds; until then its moves are essentially random. This exploratory phase may be reduced significantly in a certain class of games using RAVE (Rapid Action Value Estimation). In these games, permutations of a sequence of moves lead to the same position. Typically, they are board games in which a move involves placement of a piece or a stone on the board. In such games the value of each move is often only slightly influenced by other moves.

In RAVE, for a given game tree node $N$ , its child nodes $C i$ store not only the statistics of wins in playouts started in node $N$ but also the statistics of wins in all playouts started in node $N$ and below it, if they contain move $i$ (also when the move was played in the tree, between node $N$ and a playout). This way the contents of tree nodes are influenced not only by moves played immediately in a given position but also by the same moves played later.

RAVE on the example of tic-tac-toe. In red nodes, the RAVE statistics will be updated after the b1-a2-b3 simulation.

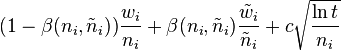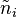When using RAVE, the selection step selects the node, for which the modified UCB1 formula $(1-\beta(n_i, \tilde{n}_i))\frac{w_i}{n_i} + \beta(n_i, \tilde{n}_i)\frac{\tilde{w}_i}{\tilde{n}_i} + c\sqrt{\frac{\ln t}{n_i}}$ has the highest value. 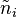In this formula, $\tilde{w}_i$ and $\tilde{n}_i$ stand for the number of won playouts containing move $i$ and the number of all playouts containing move $i$ , and the $\beta(n_i, \tilde{n}_i)$ function should be close to one and to zero for relatively small and relatively big $n i$ and $\tilde{n}_i$ , respectively. One of many formulas for $\beta(n_i, \tilde{n}_i)$ , proposed by D. 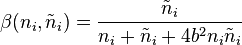Silver, says that in balanced positions one can take $\beta(n_i, \tilde{n}_i)=\frac{\tilde{n}_i}{n_i+\tilde{n}_i+4b^2 n_i\tilde{n}_i}$ , where $b$ is an empirically chosen constant.

Heuristics used in Monte Carlo tree search often require many parameters. There are automated methods to tune the parameters to maximize the win rate.

Monte Carlo tree search can be concurrently executed by many threads or processes. There are several fundamentally different methods of its parallel execution:

Leaf parallelization, i.e. parallel execution of many playouts from one leaf of the game tree.
Root parallelization, i.e. building independent game trees in parallel and making the move basing on the root-level branches of all these trees.
Tree parallelization, i.e. parallel building of the same game tree, protecting data from simultaneous writes either with one, global mutex, with more mutexes, or with non-blocking synchronization.

History

The Monte Carlo method, based on random sampling, dates back to the 1940s. Bruce Abramson explored the idea in his 1987 PhD thesis and said it "is shown to be precise, accurate, easily estimable, efficiently calculable, and domain-independent."

The rating of best go-playing programs on the KGS server since 2007. Since 2006, all the best programs use Monte Carlo tree search.

Monte Carlo tree search has also been used in programs that play other board games (for example Hex,).

GO.BA.net